Линейная функция

Линейной функцией называется такая функция, которая задана формулой y = kx + b, где k и b - действительные числа. Если, в частности, k = 0, то получаем постоянную функцию у = b.

Постоянная функция.

Постоянной называется функция, заданная формулой у = b, где b - некоторое число.

Графиком постоянной функции у = b является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат. На рисунке изображены графики нескольких постоянных функций. В частности, графиком функции y = 0 является ось абсцисс.

Если b = 0, то получаем прямую пропорциональность у = kх.

Прямая пропорциональность.

Прямой пропорциональностью называется функция, заданная формулой у = kх,
где k ≠ 0. Число k называется коэффициентом пропорциональности.

Перечислим свойства функции у = kх.
1) Область определения функции - множество всех действительных чисел.
2) у = kх - нечетная функция (f (- х) = k (- х) = - kх = - f (x)).
3) При k > 0 функция возрастает, а при k < 0 убывает на всей числовой прямой.

На рисунке а) изображен график функции у = kх при k > 0, а на рисунке б) - график функции у = kх при k < 0.

Перечислим свойства линейной функции у = kх + b при k ≠ 0, b ≠ 0.
1) Область определения функции - множество всех действительных чисел.
2) Функция у = kх + b ни четна, ни нечетна.
3) При k > 0 функция возрастает, а при k < 0 убывает на всей числовой прямой.

Графиком функции у = kх + b является прямая, параллельная графику прямой пропорциональности у = kх.

На рисунке изображен график функции у = kх + b. Это прямая, параллельная прямой, служащей графиком функции у = kх, и проходящая через точку (0; b) на оси ординат.

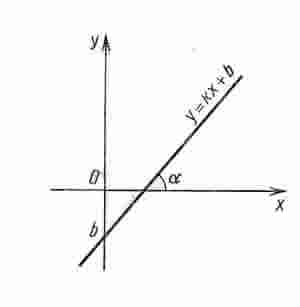
Число k называется угловым коэффициентом прямой, оно равно тангенсу угла между прямой и положительным лучом оси х, т. е. k = tgα.

Взаимное расположение графиков линейных функций.

Пусть даны две линейные функции у = k₁х + b₁ и у = k₂x + b₂. Их графиками служат прямые. Эти прямые пересекаются, если k₁ не равно k₂ (рис. а). Прямые параллельны, если k₁ = k₂. Последний случай, в свою очередь, можно разбить на два: если k₁ = k₂ и b₁ = b₂, то прямые совпадают; если k₁ = k₂ и b₁ не равно b₂, то прямые параллельны и не совпадают (рис. б).

Обратная пропорциональность.

Обратной пропорциональностью называют функцию, заданную формулой y = k/x,
где k ≠ 0. Число k называют коэффициентом обратной пропорциональности.

Перечислим свойства функции у = k/x .
1) Область определения - множество всех действительных чисел, кроме нуля.
2) у = k/x - нечетная функция (поскольку f (-x) = k/(- x)= - k/x = - f (x)).
3) Если k > 0, то функция у = k/x убывает на ( - ∞; 0) и (0; + ∞). Если k < 0, то функция у = k/x возрастает на ( - ∞; 0) и ( 0; + ∞).

Если k < 0, то ветви графика обратной пропорциональности расположены во II и IV координатных четвертях, когда k > 0 ветви графика обратной пропорциональности расположены в I и III координатных четвертях.

Квадратичная функция.

Функция у = ах² + bх + с (а, b, с - постоянные величины, а ≠ 0) называется квадратичной. В простейшем случае у = ах² (b = с = 0) график есть кривая линия, проходящая через начало координат.

Кривая, служащая графиком функции у = ах², есть парабола. Каждая парабола имеет ось симметрии, называемую осью параболы. Точка О пересечения параболы с ее осью называется вершиной параболы.

График функции у = аx² + bх + с имеет ту же форму, что и график функции у = ах² (при том же значении a), т е. также есть парабола. Ось этой параболы по-прежнему вертикальна, но вершина лежит не в начале координат, а в точке ( - b/(2a); c - b²/(4a) ).

Степенная функция с натуральным показателем.

Функция у = хⁿ, где n - натуральное число, называется степенной функцией с натуральным показателем.
При n = 1 получаем функцию у = х.
При n = 2 получаем функцию у = х².

Перечислим свойства функции у = х².
1) Область определения функции - вся числовая прямая.
2) у = х² - четная функция (f ( - х) = ( - х)² = х² = f (x)).
3) На промежутке [0; + ∞) функция возрастает (если 0 ≤ х₁ < х₂ , то х₁² < х₂², а это и означает возрастание функции).
4) На промежутке ( - ∞ ; 0] функция убывает ( если x₁ < x₂ ≤ 0, то х₁² > х₂² , а это и означает убывание функции).

Графиком функции у = х² является парабола (см. рис).

При n = 3 получаем функцию у = х³.

Перечислим свойства функции у = х³.
1) Область определения функции - вся числовая прямая.
2) у = х³ - нечетная функция (f (- х) = (- х)³= - х³ = - f (x))
3) Функция у = х³ возрастает на всей числовой прямой.
График функции у = х³ изображен на рисунке. Он называется кубической параболой.

Пусть n - произвольное четное натуральное число, большее двух: n = 4, 6, 8, ... . В этом случае функция у = хⁿ обладает теми же свойствами, что и функция у = х². График такой функции напоминает параболу у = х², только ветви графика при |x| > 1 тем круче идут вверх, чем больше n, а при |x| < 1 тем "теснее прижимаются" к оси х, чем больше n. (рис. а)

Пусть n - произвольное нечетное число, большее трех: n = 5, 7, 9, … . В этом случае функция у = хⁿ обладает теми же свойствами, что и функция у = х³. График такой функции напоминает кубическую параболу (только ветви графика тем круче идут вверх, вниз, чем больше n) (рис. б). Отметим также, что на промежутке (0; 1) график степенной функции у = хⁿ тем медленнее отдаляется от оси х с ростом х, чем больше n.

Рассмотрим функцию у = х ^-n, где n - натуральное число.
При n = 1 получаем у = х ^-1 или у = 1/х. Свойства этой функции рассмотрены выше.

Пусть n - нечетное число, большее единицы, n = 3, 5, 7, …
В этом случае функция у = х ^-n обладает в основном теми же свойствами, что и функция у = 1/х. График функции у = х ^-n (n = 3, 5, 7, …) напоминает график функции у = 1/х (рис. а).

Пусть n - четное число, например n = 2.
Перечислим некоторые свойства функции у = х ^-2, т. е. функции у = 1/х².
1) Функция определена при всех x ≠ 0
2) y =1/х² - четная функция.
3) y = 1/х² убывает на (0; + ∞) и возрастает на ( - ∞; 0).

Теми же свойствами обладают любые функции вида у = х ^-n при четном n, большем двух.

График функции у = 1/х² изображен на рисунке б. Аналогичный вид имеет график функции у = х ^-n, если n = 4, 6, ...

Перечислим свойства функции у = .
1) Область определения - луч [0; + ∞). Это следует из того, что выражение определено лишь при х ≥ 0.
2) Функция у = ни четна, ни нечетна.
3) Функция у = возрастает на луче [0; + ∞).
График функции у = изображен на рисунке а..

При четном n функция y = обладает теми же свойствами, что и функция у = , и график ее напоминает график функции у = .
При нечетном n функция у = обладает теми же свойствами, что и функция у = , и график ее напоминает график функции у = .

Рассмотрим функцию у = х^r, где r - положительная несократимая дробь.
Перечислим некоторые свойства этой функции.
1) Область определения - луч [0; + ∞).
2) Функция ни четная, ни нечетная.
3) Функция у = х^r возрастает на [0; + ∞).

Он заключен между графиками функций у = х² и у = х³, заданных на промежутке [0; + ∞).
Подобный вид имеет график любой функции вида у = х^r, где r > 1.
На рисунке б изображен график функции у = х^2/3. Подобный вид имеет график любой степенной функции у = х^r, где 0 < r < 1.

Рассмотрим функцию у = х ^-r, где r - положительная несократимая дробь.

Перечислим свойства этой функции.
1) Область определения - промежуток (0; + ∞).
2) Функция ни четная, ни нечетная.
3) Функция у = х ^-r убывает на (0; + ∞)

Показательная функция.

Показательная функция задается формулой у = а^х, где а > 0 и а ≠ 1.

Перечислим свойства функции у = а^х при а > 1.
1) Область определения функции - вся числовая прямая.
2) Область значений функции - промежуток (0; + ∞).
3) Функция не является ни четной, ни нечетной. Это следует из того,
что а ^-х ≠ а^х и а ^-х ≠ - а^х.
4) Функция возрастает на всей числовой прямой.

График функции у = а^х при а > 1 выглядит так, как показано на рисунке. Отметим, что эта функция принимает любые положительные значения.

Свойства функции у = а^х при 0 < а < 1.
1) Область определения функции - вся числовая прямая.
2) Область значений - (0; + ∞).
3) Функция не является ни четной, ни нечетной.
4) Функция убывает на всей числовой прямой.

График функции у = а^х при 0 < а < 1 выглядит так, как показано на рисунке. Отметим, что эта функция принимает любые положительные значения.

Логарифмическая функция.

Логарифмическая функция у = log_a x обладает следующими свойствами :
1) Область определения - (0; + ∞).
2) Область значений - ( - ∞; + ∞)
3) Функция ни четная, ни нечетная.
4) Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0 < а < 1.

График функции у = log_a x может быть получен из графика функции у = а^х с помощью преобразования симметрии относительно прямой у = х. На рисунке а построен график логарифмической функции для а > 1, а на рисунке б - для 0 < a < 1.

Среди показательных функций у = а^х, где а > 1, особый интерес для математики и ее приложений представляет функция, обладающая следующим свойством: касательная к графику функции в точке (0; 1) образует с осью х угол 45°. Основание а такой функции ах принято обозначать буквой е, т. е. у = е^х. Подсчитано, что е = 2, 7182818284590..., и установлено, что е - иррациональное число. Логарифмическую функцию, обратную показательной функции у = е^х, т. е. функцию у = log_е x, принято обозначать у = ln х
(ln читается "натуральный логарифм"). График функции у = ln х изображен на рисунке.

Тригонометрические функции.

Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.
Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная.

Свойства и график функции y = sin х.
1) Область определения - множество всех действительных чисел.
2) Область значений - отрезок [ - 1; 1].
3) Функция периодическая; основной период равен 2π.
4) Функция нечетная .
5) Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Z. График функции у = sin х изображен на рисунке.

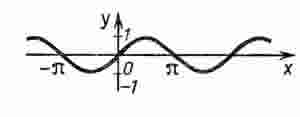
Свойства и график функции у = cos х.
1) Область определения функции - множество всех действительных чисел.
2) Область значений - отрезок [- 1; 1].
3) Функция периодическая с основным периодом 2π.
4) Функция четная.
5) Функция убывает на промежутках [2πn; π+ 2 n] и возрастает на промежутках [-π+ 2πn; 2πn], nπZ.
График функции у = соs х изображен на рисунке.

Свойства и график функции у = tg x.
1) Область определения: xπ/2 + πk, kZ.
2) Область значений - вся числовая прямая.
3) π- основной период функции.
4) Функция нечетная.
5) Функция возрастает на промежутках ( -π/2 +πn;π/2 +πn).
График функции у = tg х изображен на рисунке.

Свойства и график функции у = ctg х.
1) Область определения функции: xπ/2 +πk, kZ.
2) Область значений функции - вся числовая прямая.
3) Функция периодическая с основным периодом π.
4) Функция нечетная.
5) Функция у = ctg х убывает на промежутках (πn;π+πn).
График функции у = ctg х изображен на рисунке.