Введение
Определение
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом, а переменную у - зависимой переменной. Значение у, соответствующее заданному значению х, называют значением функции.
Записывают: у = f (х). Буквой f обозначается данная функция, т. е. функциональная зависимость между переменными х и у; f (х) есть значение функции, соответствующее значению аргумента х. Говорят также, что f (х) есть значение функции в точке х.
Все значения, которые принимает независимая переменная, образуют область определения функции.
Все значения, которые принимает функция f (х) (при х, принадлежащих области ее определения), образуют область значений функции. G
Способы задания функции.
1. Аналитический способ
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х),
где f (х) - некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
Для аналитически заданной функции иногда не указывают явно область определения функции. В таком случае подразумевают, что область определения функции у = f (х) совпадает с областью определения выражения f (х), т. е. с множеством тех значений х, при которых выражение f (х) имеет смысл.
2. Табличный способ
На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов, таблица квадратных корней.
Во многих случаях табличное задание функции оказывается удобным. Оно позволяет найти значения функции для значений аргумента, имеющихся в таблице, без всяких вычислений. На практике часто зависимость одной величины от другой находят опытным путем. В этом случае одной величине придают определенные значения, а потом из опыта для каждого из таких значений находят значение (обычно приближенное) второй величины. Таким образом опыт позволяет составить некоторую таблицу значений функции. Существуют методы, позволяющие по такой таблице подбирать формулы, задающие функции (с определенной точностью). G
График функции.
Пусть функция задана аналитически формулой у = f (х). Если на координатной плоскости отметить все точки, обладающие следующим свойством: абсцисса точки принадлежит области определения функции, а ордината равна соответствующему значению функции, то множество точек (х; f (x)) есть график функции.
На практике для построения графика функции составляют таблицу значений функции при некоторых значениях аргумента, наносят на плоскость соответствующие точки и соединяют полученные точки линией. При этом предполагают, что график функции является плавной линией, а найденные точки достаточно точно показывают ход изменения функции.
Преимуществом графического изображения по сравнению с табличным являются его наглядность и легкая обозримость; недостатком - малая степень точности. Большое практическое значение имеет удачный выбор масштабов. По графику можно найти (приблизительно) значение функции и для тех значений аргумента, которые не помещены в таблице.G
Четные и нечетные функции.
Функция у = f (х) называется четной, если для любого х из области определения функции выполняется равенство f (- х) = f (x).
Функция у = f (х) называется нечетной, если для любого х из области определения функции выполняется равенство f (- x) = - f (x).
Например, у = х2, у = х4, у = x6 - четные функции, а у = х3, у = х5, у = х7 - нечетные функции.
Если функция у = f (х) такова, что хотя бы для одной пары значений х и -х оказалось, что f (-х) ≠ f (х), и хотя бы для другой пары значений х и - х оказалось, что f (- х) = f (х), то функция не является ни четной, ни нечетной.
Из определения следует, что область определения X как четной, так и нечетной функции должна обладать следующим свойством: если х ![]() Х, то и - х
Х, то и - х ![]() Х (т. е. X - симметричное относительно 0 множество).
Х (т. е. X - симметричное относительно 0 множество).
График четной функции. График нечетной функции.
Графики четной и нечетной функций обладают следующими особенностями:
Если функция является четной, то ее график симметричен относительно оси ординат.
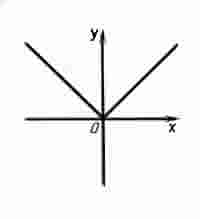
Если функция является нечетной, то ее график симметричен относительно начала координат.
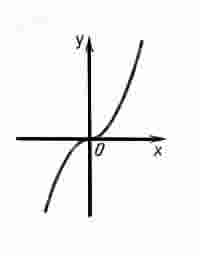
G
Периодические функции.
Функция у = f (х) называется периодической, если существует такое отличное от нуля число Т, что для любого х из области определения функции справедливо равенство f (х + Т) = f (х) = f (x - Т).
Число Т называется периодом функции у = f (х).
Из этого определения сразу следует, что если Т - период функции у = f (х), то 2Т, ЗТ, 4Т, -Т, -2 Т, - 3Т, - 4Т - периоды функции. Значит, у периодической функции бесконечно много периодов. Если, например, Т - период функции, то и число вида kТ, где k - любое целое число, также является периодом функции.
Чаще всего (но не всегда) среди множества положительных периодов функции можно найти наименьший. Его называют основным периодом.
Графики периодических функций обладают следующей особенностью. Если Т - основной период функции у = f (х), то для построения ее графика достаточно построить ветвь графика на одном из промежутков оси х длиной Т, а затем осуществить параллельный перенос этой ветви по оси х на ±Т, ± 2Т, ± ЗТ...

Чаще всего в качестве такого промежутка длиной Т выбирают промежуток с концами в точках ( - Т/2 ; 0) и ( Т/2 ; 0) или (0; 0) и (T; 0).G
Монотонные функции.
Функция у = f (х) называется возрастающей на промежутке X, если для любых х1 и х2 из X, таких, что х1 < х2, выполняется неравенство f (х1) < f (х2) (короче: х1 < x2 => f (х1) < f (х2)). Функция у = f (х) называется убывающей на промежутке X, если для любых х1 и х2 из X,таких, что x1 < x2, выполняется неравенство f (х1) > f (х2) (короче: х1 < x2 => f (х1) > f (х2)). Иными словами, функция возрастает (убывает) на промежутке X, если, какие бы два значения аргумента, принадлежащие этому промежутку, ни взять, окажется, что большему значению аргумента соответствует большее (меньшее) значение функции.
При движении вдоль оси абсцисс слева направо ордината графика возрастающей функции увеличивается (рис. а), а ордината графика убывающей функции уменьшается (рис.б).
Возрастающие и убывающие функции объединяются термином "монотонные функции".

G
Касательная к графику функции.
Касательной к графику функции у = f (х), дифференцируемой в точке х = а, называется прямая, проходящая через точку (0; f (а)) и имеющая угловой коэффициент f' (а).
k = f' (а), т. е. значение производной функции у = f (х) в точке х = а равно угловому коэффициенту касательной к графику функции у = f (х} в точке х = а (рис. а). В этом состоит геометрический смысл производной.

Если функция у = f (x) дифференцируема в точке х = а, то в этой точке к графику можно провести касательную; верно и обратное: если в точке х = а к графику функции y = f (х) можно провести невертикальную касательную, то функция дифференцируема в точке х.
Это позволяет по графику функции находить точки, в которых функция имеет или не имеет производную. Так, функция, график которой изображен на рисунке б, дифференцируема во всех точках, кроме точки х = 1; в этой точке график имеет заострение и касательную провести нельзя.

Уравнение касательной к графику функции y = f (x) в точке х = а имеет вид:
y = f (a) + f '(а) (x - a).
G
Способы задания
График функции
Четные и нечетные функции
Периодические функции
Монотонные функции
Касательная
Обратная пропорциональность
Квадратичная
Степенная
Показательная
Логарифмическая
Тригонометрическая
Квадратные
Показательные
Логарифмические
Тригонометрические